La distributivité

I - Le développement

a) Définition du développement

Deévelopper le produit A x B revient à le mettre sous la forme d'une somme algébrique.

Exemple : 

5 (3x - 5) peut s'écrire 15x - 25, c'est à dire sous la forme d'une somme algébrique.

b) La simple distributivité

1 - La multiplication distributive par rapport à l'addition

K (a+b) = K x a + K x b

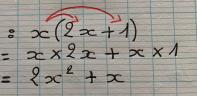
2 - La multiplication distributive par rapport à la soustraction

K (a-b) = K x a - K x b

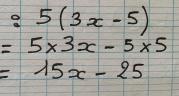
c) La double distributivité

(a+b) (c+d) = a x c + a x d + b x c + b x d

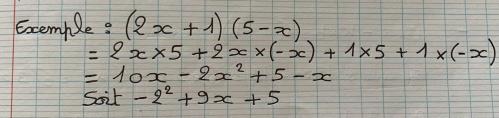
II - La factorisation

La factorisation est utilisée pour simplifier des sommes algébriques en produits de facteurs.

a) Définition de la factorisation

Exemple :

12x + 5x est une somme algébrique qui correspond à 12 X x + 5 X x

En écrivant 17x on l'a transformée en un produit

Attention la factorisation est le procédé inverse du dévelopemment

b) Les formules de factorisation

1 - Les deux formules découlant de la simple distributivité

- k x a + k x b = k (a+b)

Exemple : 18x + 12 = 6 x 3x + 6 x 2 = 6 (3x + 2)

- k x b = k (a - b)

Exemple : 18x - 12 = 6 x 3x - 6 x 2 = 6 (3x - 2)

Pour factoriser une expression, on peut identifier un facteur commun à chaque terme de la somme lorsqu'il en existe un.

2 - La factorisation a² - b²

a² - b² = (a-b) (a+b)

Exemple : 

x² - 16

x² - 4²

(x-4) (x+4)